Act 1
- How many bumps are on the entire bridge?
- Write down a guess.
Act 2
3. What information would be useful to figure this out?
4. Write down some questions you have in your head right now.
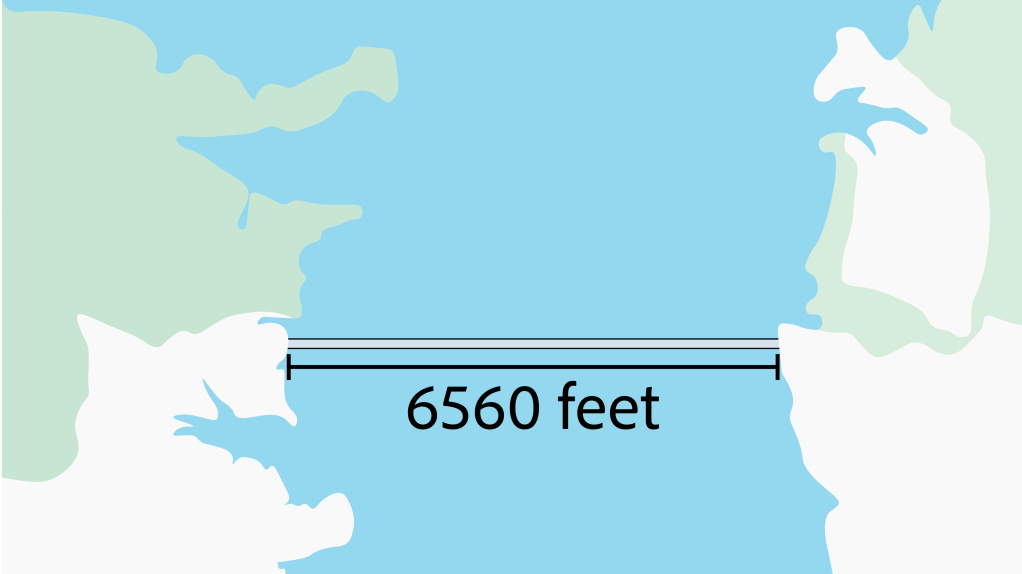
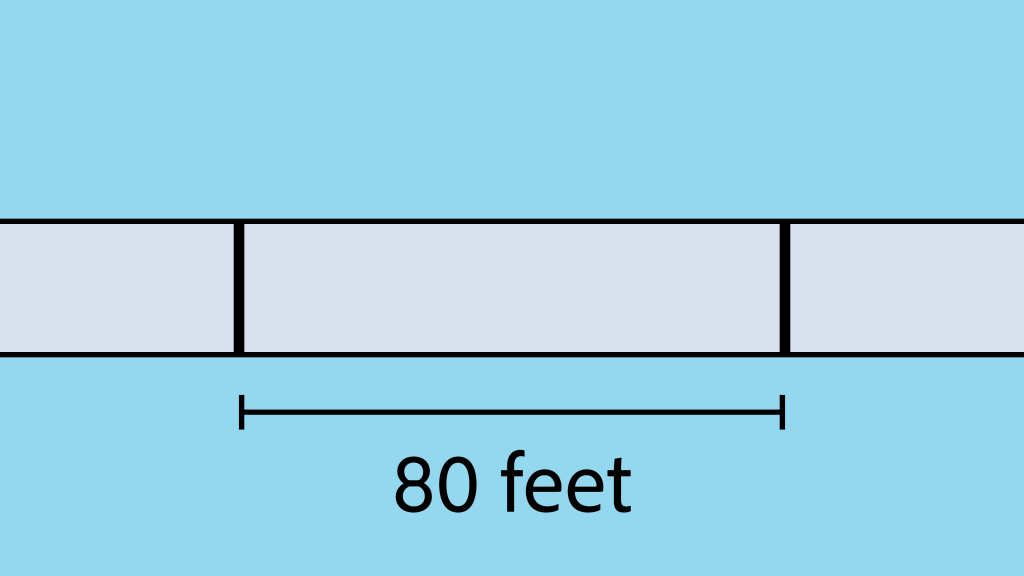
Act 3
Sequel
5. How many bumps would there be on a bridge that is 4,640 feet long?
6. How long would a bridge with 43 bumps be?
Common Core Standards
Find whole-number quotients of whole numbers with up to four-digit dividends and two-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
TEKS
Represent quotients of decimals to the hundredths, up to four-digit dividends and two-digit whole number divisors, using objects and pictorial models, including area models
When Math Happens 