Act 1
1. How far away is he from the hole?
2. Write down a guess.
Act 2
3. What information would be useful to figure this out?
4. Write down some questions you have in your head right now.
The students need to know the dimensions of whatever triangle the announcer used to make his calculation. However, instead of immediately giving two sides and an unknown, I think it would be neat to allow the kids to use a little reasoning. Therefore, I’d put this image in front of them first.
This is the same image from the Act 1 video. My vision is for the students to try to figure out where the announcer formed his triangle. I want the kids to visualize possible shapes and talk about why some may or may not work. This could lead to a good discussion. For example, why doesn’t this one work…
What do you think about this one…
It looks pretty close, but how can we figure out if it’s an acceptable triangle? You could ask again what information could be useful to analyze this triangle and use this Desmos graph to find that information.
After the side lengths are determined, the kids can do calculations to prove whether or not it’s truly a right triangle. The students can also form other triangles in Desmos as well to test their initial reasoning. Overall, the discussion can help reinforce the fact that a right triangle is necessary for the Pythagorean Theorem to work, and it also allows the students to play with the math a bit before jumping into the given triangle and dimensions.
Next, I’d show this image and have the class estimate the missing sides.
Again, I’m trying to allow for as much notice and wonder as possible. Before giving the class all of the dimensions, it would be great for the kids to make an even more precise estimate to compare with their eventual calculation.
At this point, we’re ready for the final image.
Let the Pythagorean Theorem begin.
Act 3
Sequel
5. Draw a different triangle where the shot length is the hypotenuse. What are some possible dimensions?
6. How can you prove that your new triangle is a right triangle?
8.G.B.7
Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
HSG.SRT.C.8
Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems.
8.7(C)
Use the Pythagorean theorem and its converse to solve problems
G.6(D)
verify theorems about the relationships in triangles, including proof of the Pythagorean Theorem, the sum of interior angles, base angles of isosceles triangles, midsegments, and medians, and apply these relationships to solve problems
Credits: ESPN, theopen.com




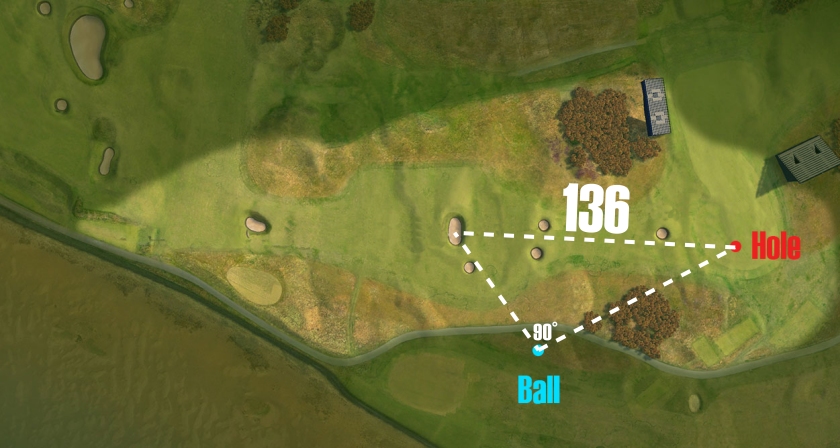


In the final image, how do you know the one leg is 91 yards long? Where does that information come from?
On the golf course’s website, they show that the fairway bunker is 136 yards from the hole. From there, I assumed that the announcers did their math right for the distance from the ball to the hole (101 yards). Based on that information, I calculated the other leg and got 91 yards. It may not be correct in real life, but I just wanted the math to workout for the problem based on the video.
Thanks for the great problem. Question–if we use the right triangle shown, we know the side that is 95 yards from the fairway to the hole. Do you have students just estimate the distance from the ball to the 95 yards point (it looks about 36 yards), or do you use the Desmos plot and a proportion to figure this? Just curious where the second side length came from to get the hypotenuse distance to the hole.
Thanks for the kind words and the question. For this problem, I’d use this image to have the kids calculate the distance from the ball to the hole. I used the golf course’s website to get the 136 yards, and I assumed that the announcers were right that the ball was 101 yards from the hole. From there, I just used the Pythagorean Theorem to get the 91 yards.
For your question, I like the idea of having students estimate the distance based on other distances given. From there, they can do calculations and see if the answer seems reasonable. After estimation, I’d give them more information or use Desmos and a proportion.
Overall, all the side lengths I gave either came from the golf course website or calculations based on the assumption that the announcers were right. Hope that answered your question!